Intrebari de zgariat neuronii (III)
marți, aprilie 4, 2017 16:33- Câte submulțimi are o mulțime?
Raspuns
Mulțimea este o colecție (grup) formată din obiecte diferite, aceste obiecte ale mulțimii numindu-se elemente. Numărul elementelor unei mulțimi se numește cardinalul mulțimii. O mulțime se notează, de regulă, cu o literă mare din alfabetul latin. Dacă mulțimea A are 3 elemente, atunci card A = 3, unde card A este noatația pentru cardinalul mulțimii A. Fie A și B două mulțimi. Spunem că mulțimea A este inclusă în mulțimea B sau că A este o submulțime a mulțimii B dacă orice element din A este și element în B (toate elementele mulțimii A aparțin și mulțimii B). Se notează A⊂B (se citește A inclusă în B) sau B⊃A (se citește B include A). Ajungând la întrebare, răspunsul este dat de următoarea teoremă:Numărul submulțimile unei mulțimi cu n elemente (n≥0) este egal cu 2n.
Câteva observații:
- Orice mulțime nevidă are cel puțin două submulțimi: mulțimea vidă (mulțimea fără nici un element) și mulțimea însăși. Evident, mulțimea vidă are o singură submulțime: mulțimea vidă.
- Mai multe despre mulțimi găsiți aici.
Să încercăm să demonstrăm teorema amintită anterior. Vom folosi metoda inducției matematice. Notăm P(n) afirmația teoremei.
- Verificăm dacă P(n) este adevărată pentru n = 0. Dacă n = 0, atunci mulțimea nu are elemente, adică este egală cu mulțimea vidă, iar mulțimea vidă are 20 = 1 submulțimi, adică o singură submulțime (mulțimea vidă).
- Să demonstrăm că P(k) =>P(k + 1), adică dacă P(k) este adevărată, atunci și P(k + 1) este adevărată. Dacă n = k, atunci avem 2k submulțimi ale mulțimii date (formată din k elemente). Dacă mulțimea are k + 1 elemente, atunci cu al k + 1 – lea element, adăugat celor 2k submulțimi, se mai formează 2k submulțimi, adică pentru n = k + 1, avem 2K + 2K = 2k + 1 submulțimi. Și teorema este demonstrată.
De exemplu, mulțimea cu un element are două submulțimi, cea cu două elemente are 4 submulțimi, cea cu 3 elemente are 8 submulțimi, cea cu 4 elemente are 16 submulțimi etc.
- Cum demonstrăm că numărul 10n + 18n – 28 este divizibil cu 27, pentru orice n număr natural, n>0?
- Raspuns
Demonstrația se bazează pe principiul inducției matematice (primul principiu de inducție). Iată, mai jos, în ce constă metoda inducției matematice.
Fie P(n) o propoziție matematică ce depinde de numărul natural n, n≥m, m fiind un număr natural fixat. Pentru a demonstra prin metoda inducției matematice că propoziția P(n) este adevărată parcurgem două etape:- Verificăm dacă P(m) este adevărată.
- Presupunem că P(k) este adevărată și demonstrăm că P(k + 1) este adevărată, unde k este un număr natural, k≥m.
În cazul întrebării de mai sus, m = 1. Să parcurgem așadar cele două etape.
- Verificăm dacă P(1) este adevărată: 101 + 18∙1 – 28 = 0 și cum 0 se divide cu 27 => P(1) este adevărată.
- Presupunem că P(k) este adevărată (k≥1) și demonstrăm că P(k+1) este adevărată. Din faptul că P(k) este adevărată, avem că numărul 10k + 18n – 28 este divizibil cu 27, adică 10k + 18k – 28 = 27p, unde p este un număr natural. De aici obținem 10k = – 18k + 28 + 27p (1). Să arătăm că 10k+1 + 18(k+1) – 28 se divide cu 27.
10k+1 + 18(k+1) – 28 = 10k x 101 + 18k + 18 – 28. Folosind relația (1), vom înlocui 10k cu – 18k + 28 + 27p. În acest fel avem: 10k+1 + 18(k+1) – 28 = (- 18k + 28 + 27p) x 10 + 18k – 10 = – 180k + 280 + 270p + 18k – 10 = – 162k + 270 + 270p = 27(- 6k + 10 + 10p), adică 10k+1 + 18(k+1) – 28 se divide cu 27, iar de aici avem că P(k + 1) este adevărată.
Fiind parcurse cele două etape, putem afirma că 10n + 18n – 28 este divizibil cu 27, pentru orice n număr natural, n>0.
- Un dreptunghi este inscris intr-un cerc cu raza de 50 m. Diferenta lungimilor laturilor dreptunghiului este de 20 m. Ce lungimi au laturile dreptunghiului?
Raspuns
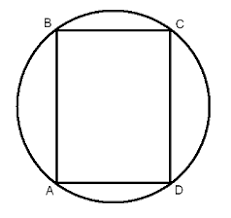
Dreptunghiul este un patrulater inscriptibil, punctul de intersecție al diagonalelor fiind centru cercului circumscris dreptunghiului. Este inscriptibil dreptunghiul deoarece, de exemplu, unghiurile opuse suplementare, adică suma măsurilor a două unghiuri opuse este de 1800. Să notăm cu L și l dimensiunile dreptunghiului, R fiind raza cercului circumscris dreptunghiului. Din enunțul problemei avem R = 50, L – l = 20 (unitatea de măsură comună fiind metrul). Cum punctul de intersecție al diagonalelor este mijlocul fiecărei diagonale, dreptunghiul fiind un paralelogram particular, avem 2R lungimea unei diagonale. Aplicând teorema lui Pitagora în triunghiul dreptunghic cu catetele L și l, ipotenuza fiind o diagonală (2R), avem:
(1) L2 + l2 = (2R) 2
Cum R = 50, L = 20 + l, înlocuind în (1) avem:
(20 + l)2 + l2 = 100 2 => 202 + 40l + l2 + l2 = 10000 =>2l2 + 40l + 400 = 10000|-10000 => 2l2 + 40l – 9600 = 0|:2 => l2 + 20l – 4800 = 0
Și am ajuns la această ecuație de gradul doi. Se poate rezolva în mai multe moduri. Să încercăm prin descompunere în factori.
l2 + 80l – 60l – 4800 = 0 => (l2 + 80l) – (60l + 4800) = 0.
Scoțând factor comun în fiecare paranteză, avem:
L(l + 80) – 60(l + 80) = 0 => (l + 80)(l – 60) = 0 => l + 80 =0 sau l – 60 = 0 => l1 = – 80, l2 = 60.
Fiind vorba de lungimi, ce nu pot fi numere negative, avem l = 60 m =>L = 80 m.
Citeste si articolele:




Intrebari de zgariat neuronii (IV) | A șaptea dimensiune says:
ianuarie 11th, 2019 at 19:13
[…] Intrebari de zgariat neuronii (III) […]
Intrebari de zgariat neuronii (VII) | A șaptea dimensiune says:
ianuarie 11th, 2019 at 21:06
[…] Intrebari de zgariat neuronii (III) […]
Intrebari de zgariat neuronii (VIII) | A șaptea dimensiune says:
mai 19th, 2019 at 8:21
[…] Intrebari de zgariat neuronii (III) […]
Intrebari de zgariat neuronii (V) | A șaptea dimensiune says:
mai 19th, 2019 at 14:26
[…] Intrebari de zgariat neuronii (III) […]