A șaptea dimensiune

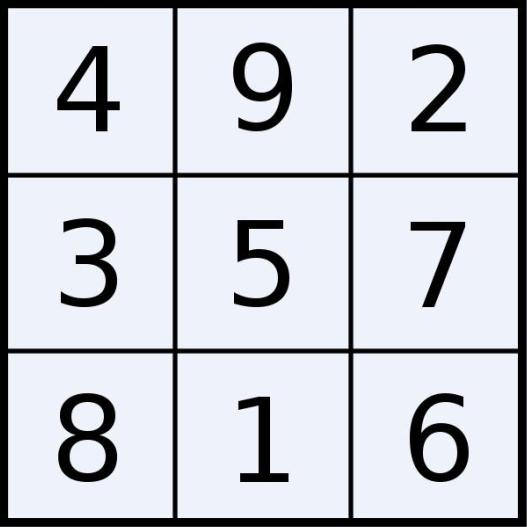Pătratul magic (sau pătratul fermecat) de ordin n este o schemă a numerelor 1, 2, 3, …, n², la care sumele de pe fiecare linie, de pe fiecare coloană şi de pe fiecare diagonală sunt egale.

Update

În China antică, se cunoșteau pătratele magice încă din Mileniul al III-lea î.Hr., după cum atestă Lo Shu. După legendă, într-o bună zi se devărsă un râu; oamenii, înfricoșați, încercară să aducă o ofrandă zeilor râului Lo (unul din cele devărsate) pentru a-i calma furia. Totuși, de fiecare dată cand făceau aceasta, apărea o broască țestoasă care încercuia ofrandele fără să le accepte, până când un băiat își dădu seama de marcajele speciale de pe carapacea ei și așa putură să ofere cantitatea cerută (15), și să mulțumească zeul, care readuse apele la nivelul lor. Au cunoscut și combinații de această clasă indienii, arabii, egiptenii și grecii.

La pătrate asemănatoare, diferitele culturi au atribuit proprietăți astrologice și divinatorii variate, fiind de numeroase ori marcate în talismane. Așa cum reia Cornelius Agrippa în Despre filozofia ocultă III (1533), pătratul de ordinul trei(15) era consacrat zeului Saturn, cel de patru(34) lui Jupiter, cel de cinci(65) lui Marte, cel de șase(111) Soare, cel de șapte(175) lui Venus, cel de opt(260) lui Mercur și cel de nouă(369) Lunei; o atribuție similară se poate găsi în astrologia hindusă. Introducerea pătratelor magice în occident se poate atribui lui Emanuel Moschopoulos, în jurul secolului al XVI-lea, autorul unui manuscris în care pentru prima oară au fost explicate câteva metode pentru a le construi. Mai târziu, studiul proprietaților acestor pătrate a atras atenția unor mari matematicieni, care au dedicat subiectului câteva opere chiar cu toată inutilitatea practică a pătratelor magice. Printre ei se pot cita Stifel, Fermat, Pascal, Leibnitz, Frenicle, Bachet, La Hire, Saurin, Euler, … se poate zice că nici un matamatician nu a putut rezista farmecelor pătratului magic.

În exemplul de mai jos, n = 4, avem 4² numere, adică 16, iar pătratul este magic. Ce numere punem în locul semnelor de întrebare?
P.S. Subiectul este, cu îngăduinţă, la nivel de clasa a V-a.

Citeste si articolele:

• Spiru Haret, universitate ilegala ce produce doua treimi din absolventii invatamantului superior din Romania
• Eroii nu mor niciodată
• Cum este Moldova de la vest de Prut? Vanghelizată şi becalizată
• Inginerul Adomniţei şi limba română
• Ce înseamnă a fi indecent