Farmecul discret al Matematicii (IV)
joi, martie 23, 2017 20:39- Marea teoremă a lui Fermat
Marea teoremă a lui Fermat este o celebră teoremă de teoria numerelor. Ea a fost enunţată de Pierre de Fermat în anul 1637, iar demonstraţia completă a fost găsită de-abia 357 de ani mai tîrziu de către matematicianul englez Andrew Wiles.
Enunţul este simplu: Ecuaţia xn + yn = zn nu are soluţii dacă n>2 este număr natural, iar x,y,z sunt numere întregi nenule.Pentru n=2 enunţul nu este adevărat. Există triplete de numere naturale (x,y,z) cu care se pot forma laturile unui triunghi dreptunghic; de aici, conform teoremei lui Pitagora, avem x2 + y2 = z2. De exemplu (3,4,5) sau (5,12,13). Există chiar o infinitate de astfel de triplete, forma lor generală fiind x = 2uv, y = u2 – v2, z = u2 + v2, unde u şi v sunt numere naturale oarecare.
Pentru n > 2, doar cazul n = 4 admite o demonstraţie elementară, schiţată de Fermat însuşi. Chiar şi pentru cazul n = 3 demonstraţia depăşeşte nivelul manualelor de liceu; primul care s-a ocupat de cazul n = 3 a fost matematicianul Leonhard Euler, în 1753. În 1825, francezii Johann Peter Gustav Lejeune Dirichlet şi Adrien-Marie Legendre tranşează cazul n = 5, demonstraţia având ca punct de plecare o idee mai veche a lui Sophie Germain. După câţiva ani, este finalizată demonstraţia pentru n = 7, de către francezul Gabriel Lamé.La mijlocul secolului XIX, Academia Franceză instituie un premiu de 3000 franci (o sumă enormă atunci) pentru o demonstraţie completă a teoremei.
Demonstraţii pentru numere prime mai mici ca 100 au fost date aproximativ în aceeaşi perioadă, de către matematicianul german Ernst Kummer.
În 1908, magnatul german Paul Wolfskehl alocă uriaşa sumă de 100.000 de mărci celui ce va demonstra teorema (‘oferta’ fiind valabilă până în 2007).
După apariţia calculatoarelor electronice, au fost abordate cazuri particulare pentru valori tot mai mari ale lui n; prin anii 1980,erau elucidate toate cazurile în care n < 4.000.000.
În ultimii ani de dinaintea găsirii demonstraţiei complete pentru orice n > 2, matematicienii erau convinşi că prin metode elementare nu se mai poate aduce nimic nou.
În anul 1983, matematicianul german Gerd Faltings a demonstrat că există cel mult o mulţime finită de contra-exemple la marea teoremă a lui Fermat.
În septembrie 1994, matematicianul englez Andrew Wiles a dat demonstraţia completă a teoremei, după ce, în 1993, propusese o altă demonstraţie, care se dovedise a fi greşită.
Informaţiile le-am luat de aici. Alte informaţii despre Marea teoremă a lui Fermat găsiţi aici (partea I) si aici (partea a II-a)
- .Ciurul lui Eratostene
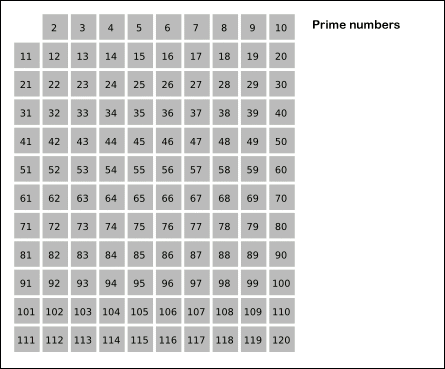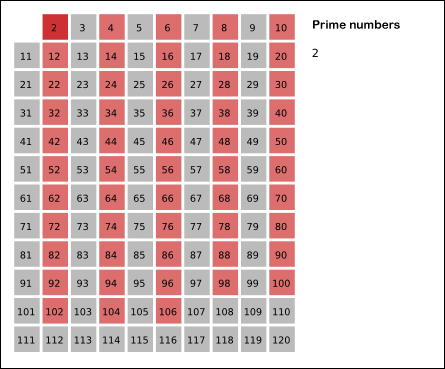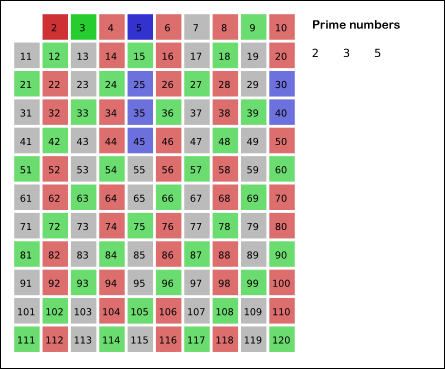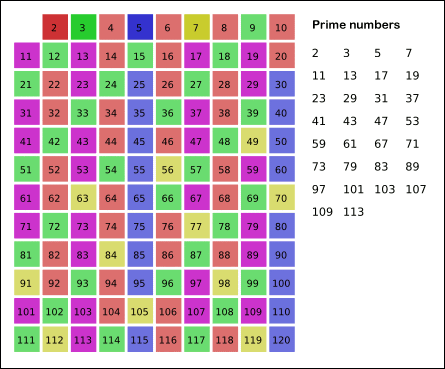
Se numeşte număr prim un număr natural diferit de 1 ce are ca divizori doar pe 1 şi numărul însuşi (are exact doi divizori). Şirul numerelor prime este infinit, 2 este singurul număr prim par (restul numerelor prime sunt impare), iar povestea numerelor prime poate merge mai departe (voi reveni asupra subiectului). O metodă simplă de a afla numerele prime până la un număr dat este Ciurul lui Eratostene. Se scrie o listă (tabel) de numere de la 2 la numărul până la care vrem să aflăm numerele prime. Se reţine 2 ca număr prim şi se marchează toţi multiplii lui 2 care, evident, nu sunt numere prime. Primul număr rămas nemarcat este 3, acesta fiind prim, şi apoi sunt marcaţi toţi multiplii lui 3, care nu sunt numere prime. Şi tot aşa. Vedeţi imaginea de mai jos.
- Sticla lui Klein
Sticla lui Klein a fost descrisă pentru prima dată în 1882 de către matematicianul german Felix Klein. Sticla lui Klein este o suprafata pe care te poti misca din exterior spre interior fara a intersecta vreo margine, o figura geometrica neorientabila, care scoate in evidenta ideea ca interiorul si exteriorul nu sunt neaparat concepte universale. Daca banda lui Moebius este o suprafat bidimensionala marginita, sticla lui Klein nu are margini.
Citeste si articolele:




Farmecul discret al Matematicii (V) | A șaptea dimensiune says:
ianuarie 11th, 2019 at 8:26
[…] Farmecul discret al Matematicii (IV) […]
Intrebari de zgariat neuronii (II) | A șaptea dimensiune says:
mai 22nd, 2019 at 19:46
[…] Farmecul discret al Matematicii (IV) […]
Intrebari de zgariat neuronii (I) | A șaptea dimensiune says:
mai 23rd, 2019 at 7:07
[…] Farmecul discret al Matematicii (IV) […]