Farmecul discret al Matematicii (I)
luni, martie 13, 2017 18:48 Despre câteva afirmații matematice (I)
Despre câteva afirmații matematice (I)
În cele ce urmează, sunt descrise câteva afirmații matematice interesante, unele dintre ele având o evoluție neașteptată, dar corectă, în timp.
Fie trinomul f(x) = x2 + x + 41. Înlocuind x cu numerele naturale 0, 1, 2, 3, …, 39 se obțin numere prime. De exemplu, f(0) = 41, f(1) = 43, f(2) = 47, f(3) = 53, f(4) = 61, f(5) = 71. Pentru x = 40, nu se mai obține un număr prim: f(40) = 402 + 40 + 41 = 40(40 + 1) + 41 = 41(40 + 1) = 412.
Matematicianul francez Pierre Fermat (1601 – 1665) a considerat numerele 220 + 1 = 3, 221 + 1 = 5, 222 + 1 = 17, 223 + 1 = 257, 224 + 1 = 6.5537, care sunt prime. Plecând de la aceste observații, Fermat a afirmat că, pentru orice număr natural n, numărul 22n + 1 este prim. Fermat nu a reușit să verifice dacă, pentru n = 5, numărul 225 + 1 = 4.294.967.297 este sau nu este prim. Peste niște ani, matematicianul elvețian Leonard Euler (1707 – 1783) a arătat că acest număr nu este prim, mai precis: 225 + 1 = 641 x 6.700.417. Ulterior s-au găsit si alte valori ale lui n, n⋲{6, 7, 8, 9, 11, 12, 18, 23, 36, 38, 73} pentru care 22n + 1 nu este prim.
Despre câteva afirmații matematice (II)
Matematicianul polonez Waclaw Sierpinski (1882 – 1969) a emis ipoteza că numărul 991n2 + 1 nu dă pătrate perfecte pentru n natural. Această afirmație s-a dovedit a fi falsă, cel mai mic număr natural n pentru care se obține pătrat perfect fiind un număr format din 29 de cifre.
Din mica teoremă a lui Fermat rezultă că dacă p ≥3 este un număr prim, atunci 2p-1 – 1 se divide cu p. Totuși, oricare ar fi numărul prim p < 1000, 2p-1 – 1 nu se divide cu p2. De aici ar putea urma că, în general, pentru nici un număr prim p, numărul 2p-1 – 1 nu se divide cu p2. S-a demonstrat, însă, ca 21093-1 – 1 se divide cu 10932.
Despre câteva afirmații matematice (III)
Fiecare număr natural par n, cu 4≤n≤20, se poate scrie ca sumă de două numere prime, care pot fi și egale. Astfel, avem: 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5, 10 = 3 + 7, 12 = 5 + 7, 14 = 7 + 7, 16 = 5 + 11, 18 = 7 + 11, 20 = 7 + 13.
Pentru orice poliedru regulat este îndeplinită relația V – M + F = 2, unde V este numărul vârfurilor, M este numărul muchiilor, iar F este numărul fețelor. Despre poliedre regulate vedeți mai multe aici. Există doar 5 tipuri de poliedre regulate și în fiecare caz relația este îndeplinită.
Pentru tetraedru: V = 4, M = 6, F = 4 (4 – 6 + 4 = 2).
Pentru cub: V = 8, M = 12, F = 6 (8 – 12 + 6 = 2).
Pentru octaedru: V = 6, M = 12, F = 8 (6 – 12 + 8 = 2).
Pentru dodecaedru: V = 20, M = 30, F = 12 (20 – 30 + 12 = 2).
Pentru icosaedru: V = 12, M = 30, F = 20 (12 – 30 + 20 = 2).
Numărul 12
Astronomii lumii antice au împărțit bolta cerească în 12 regiuni, fiecare reprezentând câte o constelație, anul a fost împărțit în 12 luni și ziua în 12×2 ore. Divinităti precum Buddha și Hristos au avut fiecare câte 12 ucenici. Unul dintre cele cinci poliedre platonice, dodecaedrul, are 12 fețe. Hexaedrul (cubul) și octoedrul, alte două poliedre regulate, au câte 12 muchii, iar icosaedrul 12 vârfuri.
Numărul 13
Numărul figurilor cărților de joc este 13. Numărul Sheherezadei conține factorul 13. 13 rotații în jurul Pământului face luna într-un an. Împreună cu numerele 14 și 15, alcătuiesc lungimile laturilor unui triunghi care are atât perimetrul, cât și aria exprimate prin numere naturale (triunghi heronic). Mari matematicieni ai Antichității, Diofante și Euclid, au scris câte 13 cărți.
Numărul 10
Toți știm că sub imperiul lui 10 stă întreaga construcție a sistemului de numerație folosit de toți locuitorii planetei: sistemul metric (multipli și submultipli) utilizează factorul 10 în transformări.
Puțini știu, însă, că din punct de vedere aritmetic, alături de numerele 1, 120, 1540 și 7140, numărul 10 este atât triunghiular, cât și tetraedral. Despre numere triunghiulare, ceva mai la vale. Ce este un număr tetraedral? Este numărul de forma n(n+1)(n+2)/6 și este dat de numărul de bile ce se pot așeza sub formă unui tetraedru.
Numărul 10 este și cel mai mic număr sumă a trei numere prime distincte: 10 = 2 + 3 + 5.
O altă proprietate surprinzătoare a numărului 10 este cea dată de egalitatea 10! = 6! ∙ 7! (Numărul n! = 1 ∙ 2 ∙ 3 ∙ … ∙ (n – 1) ∙ n) Este singurul număr cu o astfel de proprietate!
Bibliografie: Dăncilă, Ioan – Matematică distractivă, clasele a VII-a și a VIII-a, Editura ART, București, 2012
Număr triunghiular
Un număr triunghiular este numărul de puncte dintr-un triunghi unilateral umplut uniform cu puncte. De exemplu, trei puncte pot forma un triunghi și deci 3 este un număr triunghiular.
Șirul numerelor triunghiulare pentru n = 1, 2, 3… este: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, …. (Sursa)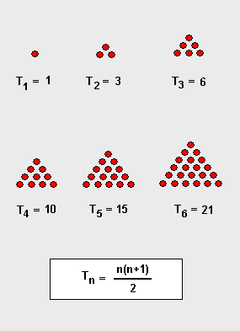
Citeste si articolele:



Farmecul discret al Matematicii (V) | A șaptea dimensiune says:
martie 16th, 2019 at 13:36
[…] Farmecul discret al Matematicii (I) […]
Farmecul discret al Matematicii (II) | A șaptea dimensiune says:
mai 25th, 2019 at 7:12
[…] Farmecul discret al Matematicii (I) […]
Farmecul discret al Matematicii (III) | A șaptea dimensiune says:
mai 25th, 2019 at 7:31
[…] Farmecul discret al Matematicii (I) […]
Farmecul discret al Matematicii (IV) | A șaptea dimensiune says:
mai 25th, 2019 at 12:11
[…] Farmecul discret al Matematicii (I) […]
Intrebari de zgariat neuronii (I) | A șaptea dimensiune says:
mai 25th, 2019 at 12:15
[…] Farmecul discret al Matematicii (I) […]